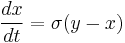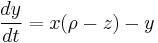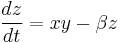Lorenz attractor

The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its figure eight shape. The map shows how the state of a dynamical system (the three variables of a three-dimensional system) evolves over time in a complex, non-repeating pattern.

Contents

Overview

The attractor itself, and the equations from which it is derived, were introduced in 1963 by Edward Lorenz, who derived it from the simplified equations of convection rolls arising in the equations of the atmosphere.

In addition to its interest to the field of non-linear mathematics, the Lorenz model has important implications for climate and weather prediction. The model is an explicit statement that planetary and stellar atmospheres may exhibit a variety of quasi-periodic regimes that are, although fully deterministic, subject to abrupt and seemingly random change.

From a technical standpoint, the Lorenz oscillator is nonlinear, three-dimensional and deterministic. For a certain set of parameters, the system exhibits chaotic behavior and displays what is today called a strange attractor. The strange attractor in this case is a fractal of Hausdorff dimension between 2 and 3. Grassberger (1983) has estimated the Hausdorff dimension to be 2.06 ± 0.01 and the correlation dimension to be 2.05 ± 0.01.

The system also arises in simplified models for lasers (Haken 1975) and dynamos (Knobloch 1981).

Equations

The equations that govern the Lorenz oscillator are:

\frac{dx}{dt} = \sigma (y - x)
\frac{dy}{dt} = x (\rho - z) - y
\frac{dz}{dt} = xy - \beta z

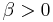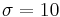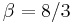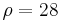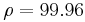where \sigma is called the Prandtl number and \rho is called the Rayleigh number. All \sigma, \rho, \beta > 0, but usually \sigma = 10, \beta = 8/3 and \rho is varied. The system exhibits chaotic behavior for \rho = 28 but displays knotted periodic orbits for other values of \rho. For example, with \rho = 99.96 it becomes a T(3,2) torus knot.

A Saddle-node bifurcation occurs at 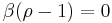\beta(\rho-1)=0. When σ ≠ 0 and β (ρ-1) ≥ 0, the equations generate three critical points. The critical points at (0,0,0) correspond to no convection, and the critical points at 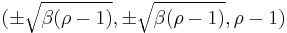(\pm\sqrt{\beta(\rho-1)}, \pm\sqrt{\beta(\rho-1)}, \rho-1) correspond to steady convection. 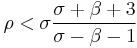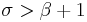This pair is stable only if \rho< \sigma\frac{\sigma%2B\beta%2B3}{\sigma-\beta-1}, which can hold only for positive \rho if \sigma > \beta%2B1.

Sensitive dependence on the initial condition
Time t=1 (Enlarge) Time t=2 (Enlarge) Time t=3 (Enlarge)
These figures — made using ρ=28, σ = 10 and β = 8/3 — show three time segments of the 3-D evolution of 2 trajectories (one in blue, the other in yellow) in the Lorenz attractor starting at two initial points that differ only by 10-5 in the x-coordinate. Initially, the two trajectories seem coincident (only the yellow one can be seen, as it is drawn over the blue one) but, after some time, the divergence is obvious.
Java animation of the Lorenz attractor shows the continuous evolution.

Rayleigh number

The Lorenz attractor for different values of ρ
ρ=14, σ=10, β=8/3 (Enlarge) ρ=13, σ=10, β=8/3 (Enlarge)
ρ=15, σ=10, β=8/3 (Enlarge) ρ=28, σ=10, β=8/3 (Enlarge)
For small values of ρ, the system is stable and evolves to one of two fixed point attractors. When ρ is larger than 24.28, the fixed points become repulsors and the trajectory is repelled by them in a very complex way, evolving without ever crossing itself.
Java animation showing evolution for different values of ρ

Source code

The source code to simulate the Lorenz attractor in GNU Octave follows.

% Lorenz Attractor equations solved by ODE Solve
%% x' = sigma*(y-x)
%% y' = x*(rho - z) - y
%% z' = x*y - beta*z
function dx = lorenzatt(X)
    rho = 28; sigma = 10; beta = 8/3;
    dx = zeros(3,1);
    dx(1) = sigma*(X(2) - X(1));
    dx(2) = X(1)*(rho - X(3)) - X(2);
    dx(3) = X(1)*X(2) - beta*X(3);
    return
end

% Using LSODE to solve the ODE system.
clear all
close all
lsode_options("absolute tolerance",1e-3)
lsode_options("relative tolerance",1e-4)
t = linspace(0,25,1e3); X0 = [0,1,1.05];
[X,T,MSG]=lsode(@lorenzatt,X0,t);
T
MSG
plot3(X(:,1),X(:,2),X(:,3))
view(45,45)

 

% A simple Lorenz Solver in MatLab code
function dxdt=myLorenz(t,x)
% The RHS of the Lorenz attractor
% Save this function in a separate file 'myLorenz.m'
sigma = 10;
r = 28;
b = 8/3;
dxdt=[ sigma*(x(2)-x(1));
(1+r)*x(1)-x(2)-x(1)*x(3);
x(1)*x(2)-b*x(3)];
end

%% Main program: Save the program in a separate .m file and run it.
clear all; % clear all variables
t=linspace(0,50,3000)'; % time variables
y0=[-1;3;4]; % Initial conditions
[t,Y] = ode45(@myLorenz,t,y0); %Invoking built-in solver 'ode45'
plot3(Y(:,1),Y(:,2),Y(:,3));  % Plot results
grid on;

See also

References

External links